Is a different treatment for cancer possible?
A technique formulated before the Second World War in Nazi Germany but summarily forgotten afterwards is becoming fashionable again. Can we cure cancer without needing to poison or burn our bodies?
If you like what you read, copy and share the link, post it on another platform.
Please also subscribe to make sure you will not miss future posts. Subscription is free. Your email will not be used for other purposes. You will receive no advertisements.
In addition to the main story on new cancer treatment methods, you will also find short takes on:
How the efficiency demonstrated by DeepSeek may upset nuclear power prospects in USA
How Stephen Baxter’s last book Galaxias was a disappointment for me
The way the humanity deals with an indifferent alien species in the Usurper of the Sun by Hosuke Nojiri
The Answer is No by Fredrik Bakman, who The Sydney Morning Herald calls Sweden’s most popular literary export since Stieg Larsson
Istanbul - Brisbane price comparison, the trend since July 2024
and the latest from Pascal and Hagi.
-+-+-+-+
Cancer is the second leading cause of death after heart attacks. I decided to prepare this post after recently learning about a fundamental difference of opinion within the medical field on what causes cancer and what the best treatment is.
One side of the argument believes in the mainstream paradigm. I use the word “belief” deliberately because, they seem to have a religious belief in the potency of their procedures and if results are not good they argue we only need to do more of the same.
The other side is rediscovering and improving a technique that was formulated before the Second World War in Nazi Germany but was summarily forgotten and set aside after the war, discredited by the proponents of the current approach.
One side sees cancer as a disease caused by gene damage and the others think it is a metabolic ailment like diabetes. These two schools of thought favour entirely different treatments to cure the same problem. This is such a fundamental point of difference on such an important topic that I cannot help being amazed that it remains unresolved.
I must admit that another reason the discussion interested me is that it is a good proxy for the broader discussion happening in the health sector at the moment. This is a discussion between the big medical and pharmaceutical complex trying to do right without hurting company profits and independent doctors and researchers trying to do right no matter what.
I wanted to learn more about it. I will start sharing my learning with you in this post. Needless to say (but I will say it anyway), being an engineer with no medical training, my guidance in trying to understand either side of this discussion is my freshman chemistry classes plus common sense. Therefore, I will write very carefully and try to present my understanding as clearly as possible. I have always believed that by trying to write clearly one clarifies their own thinking. I apologise to those who may find the pace too slow. It will still be a high-level narrative. I am hoping readers with deeper knowledge will correct or at least identify my mistakes.
Disclaimer: The purpose of this post is to reflect on the causes of cancer and the differences between the current treatment methods. Nothing you read here should be taken as specific advice for any medical condition. If you need medical advice, talk to your doctor.
We are not winning against cancer
The cancer-attributed medical costs are substantial and continue to rise. We are trying hard to defeat cancer—not only by spending vast amounts of money, but by doing so in ways that are often incredibly painful. We create highly toxic substances and inject them into our bloodstream, hoping to poison cancer cells while accepting that healthy cells and organs may also be harmed in the process. We use radiation on our bodies to target cancerous tumors, even though such treatment may destroy other tissue and might even spawn new tumors as a side effect. Like devout zealots who willingly subject themselves to punishment, we endure these torturous methods in the hope that this will help defeating this relentless disease.
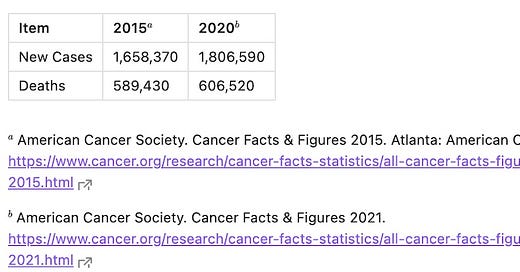
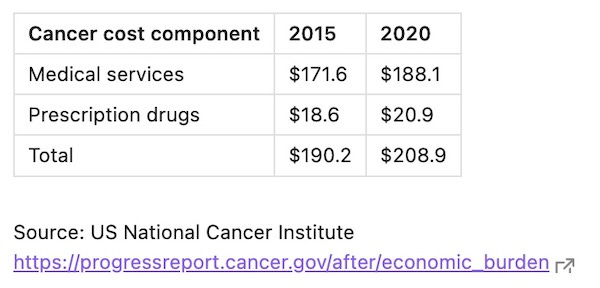
The following table compares the annual cost of medical care and prescription drugs provided to cancer patients in USA in 2015 and 2020, in billions of US dollars:
In 2015, approximately $190 billion was spent on cancer-related healthcare in the U.S., and this amount grew to $209 billion by 2020—a 10% increase. Both the number of new cases and the number of deaths increased over the same period:
We will never know what these numbers might have looked like if we had stopped spending in 2015. But, in any case, it is fair to say that, in spite of all this expoenditure, we are not winning the war against cancer.
The medical establishment says that in order to win we need to spend more. They say we need to design new treatments, now possibly with the help of AI. These new measures will include personalized drug regimens tailored to the genetic makeup of patients and their tumors. These treatments are likely to be costly, potentially reaching several hundred thousand dollars per year for a patient, with no guarantee of effectiveness, as past “miracle” drugs have often fallen short.
There is another way of combating cancer. Earlier in 20th Century, in pre-WW2 Germany, it was discovered that all types of cancer had a single weakness and this weakness could be exploited through diet and limited drug taking.
Warburg Effect
In pre-World War II Germany, scientist Otto Warburg discovered a fundamental property of all cancer cells. By targeting this property he identified the possibility of a universal treatment. He was nominated for a Nobel Prize for this discovery but did not receive it, possibly because he had already been awarded a Nobel in 1931 for another achievement. He obviously was a very smart man. If he had chosen to leave Germany before the war and gone to the USA, he probably would have become a household name like some other German emigrees but he chose to stay back in his country even though he had Jewish ancestry.
Cancer, above all other diseases, has countless secondary causes. But, even for cancer, there is only one prime cause. Summarized in a few words, the prime cause of cancer is the replacement of the respiration of oxygen in normal body cells by a fermentation of sugar.
Warburg was well-connected in the Western circles. He was good friends with Einstein. His laboratory was regularly visited by Western researchers. These visitors themselves were of very high caliber. For example, three of them went on to win Nobel Prizes later. One of them was Sir Hans Adolf Krebs, of the Krebs-cycle fame.
Shortly after WW2 we developed an amnesia on Otto Warburg and his approach to cancer. I find it difficult to understand how quickly and how perfunctorily the Warburg theory was discarded. This dismissive takedown was mainly done by two very senior US scientists, Sidney Weinhouse, a prominent cancer researcher and editor of Cancer Research, and Alan Aisenberg of Harvard Medical School. Both of them were preaching a gene-based explanation of cancer, which was opposite to Warburg’s metabolic explanation.
When the cause for the disease was explained differently, the proposed cure also had to be different. While Warburg’s metabolic explanation implied a cure through fasting and minimum medication for all types of cancer, the Weinhouse/Aisenberg gene-based explanation rejected any universal tratment and opened the way for drugs and treatment measures specifically designed for each type of cancer. It is tempting to suppose that Weinhouse and Aisenberg were motivated by pharmaceutical companies but, at that time, the pharmaceutical industry’s involvement in cancer research was not as prominent as it is today. I think it is more plausible to believe that the attack on the Warburg Effect was driven by the dazzling effect of recent genetic discoveries and evolving research priorities and grant opportunities exploiting those discoveries.
Back to the Future
The recent renewed interest in the metabolic aspects of cancer and the Warburg Effect is due to the apparent failure of other approaches tried since 1950s.
I came across this topic listening to a Peter Attia podcast interview with Professor Seyfried and my subsequent reading of Seyfried’s 2010 book. A subsequent literature search identified a relatively small number of academics working in the field. These include Jason Locasale (Duke University), Zhimin Lu (Zhejiang University), Lewis C. Cantley (retired from Harvard Medical School), Jacques Pouysségur (Research Director Emeritus of CNRS), and Thomas Seyfried (Boston College) of course. Professor Seyfield has a YouTube channel: Talking Cancer With Professor Thomas Seyfried.
If you are interested in his topic, as a non-technical and very high-level presentation, the Seyfried interview in the The Diary of a CEO YouTube channel would be a good place to start. The Peter Attia podcast interview would also be worth checking out especially because Attia pushes back against some of Seyfried’s arguments and you get a more nuanced outlook. Another one is the Seyfried interview last year on the AI and Health Care YouTube channel.
I would have watched and read on the other side of the argument. Unfortunately, I could not find a good place to start. It is possible that the mainstream practitioners hope the metabolic theory will go away if they manage to ignore it for sufficiently long. The stakes are very high, certainly for people’s reputations but, more importantly, and especially for the lifespan of cancer patients.
To understand and to assess the arguments on both sides, we have to start from what both sides on the fundamental cause for cancer.
What is the cause for Cancer?
We often hear about things that can trigger cancer, like smoking or UV light. These triggers, called carcinogens, can start the process that turns normal cells into cancerous tumors. But what's the nature of that process actually happening inside the cell? There are two main ideas: the somatic mutation theory and the metabolic theory.
Somatic Mutation Theory
This is the mainstream theory and most doctors today favour it. A somatic mutation is an alteration in the DNA that occurs after conception.
This theory says that cancer is caused by damage to our genes (DNA) that happens after we're born or even while we are still in the maternal womb.
Metabolic Theory
A metabolic disease is one caused by a disruption in the body’s normal chemical processes. Diabetes, for example, is a metabolic disease that stems from the body’s inability to process sugar.
The metabolic theory proposes that cancer may arise from broken cellular "engines" (mitochondria) that corrupt energy conversion mechanisms in a cell.
I know this probably sounds like gobbledygook to most readers but I promise I will make it clearer as we go along. At the moment, I am only interested in defining the lines of difference between the two sides of the argument and their impllications.
Why the Difference Matters
Somatic Mutation Theory (Gene Damage)
If cancer is due to genetic damage, there could be countless different cancers because there are endless ways genes can get damaged. As a result, the common approach to treatment is to identify these genetic mutations and then try to eliminate the cells carrying them. This is difficult because:
Cancer cells are tough to kill.
Healthy cells might also be harmed in the process.
Sometimes aggressive treatments help the cancer spread instead of destroying it.
A major challenge with this theory is that it doesn’t offer a single, unified explanation of how cancer cells originate or behave. Instead, it suggests we rely on past experience and trial-and-error for new or unusual cases. Historically, this is somewhat similar to how we dealt with diabetes when it was known only as an illness causing high blood sugar but with no understanding of the cause. No effective treatment existed until researchers discovered that the pancreas of diabetic patients wasn’t producing enough insulin.
Metabolic Theory (Energy Production Disruption)
The metabolic theory proposes that a healthy cell becomes cancerous because its normal energy-producing process—centered in the mitochondria—breaks down. As a result of this breakdown, the cell switches fermentation to generate energy. Fermentationdoes not need oxygen. A cancerous cell can function and proliferate even in the absence of oxygen,
This shift in the cell metabolism can lead to genetic instability and the other traits we associate with cancer. Essentially, the theory suggests that cancer cells are primarily metabolically dysfunctional rather than genetically mutated, the genetic damage occurs because of the metabolic breakdown.
Since cancer cells are the only cells that produce energy using oxygen-free fermentation, by inhibiting fermentation in the patient’s body we can starve the cancer cells to death. The healthy cells are not affected because they use oxygenated processes not fermentation.
Key Takeaway
Cancer research currently hinges on two broad views: one focuses on DNA damage, the other on metabolic disruption. Whichever view proves most accurate—or if both play a role—will continue to shape how we understand, prevent, and treat this disease.
(to be continued)
References
Seyfried, T. N., & Huysentruyt, L. C. (2013). On the origin of cancer metastasis. Critical Reviews™ in Oncogenesis, 18(1-2).
Seyfried TN, Huysentruyt LC. On the origin of cancer metastasis. Critical Reviews in Oncogenesis. 2013 .
Peter Attia interview with Seyfried, Spotify (2018)
X Gao, SM Sanderson, Z Dai, MA Reid, DE Cooper, M Lu, JP Richie Jr, ... (2019). Dietary methionine influences therapy in mouse cancer models and alters human metabolism. Nature 572 (7769), 397-401.
Steven Bartlett interview with Seyfried, Diary of a Ceo Youtube channel (2025)
Sanjay Juneja interview with Seyfried, AI and Healthcare Youtube channel (2024)
-+-+-+-+
Short Takes
DeepSeek R1 answer to the cantilever question
Remember the cantilever question I posed to Chat GPT and Claude and then DeepSeek v.3. When DeepSeek R1 came out, I tested it with the same question. As I expected, it answered correctly.
What stood out, however, was how it arrived at the answer. DeepSeek R1 “thinks out loud,” narrating its thought process as it works. It explains its approach at each step, checks intermediate results, backtracks when necessary, and even tries to anticipate the user’s intent—all before presenting its final answer, which is formatted separately from its reflections.
I’ve included the full DeepSeek response to the cantilever question as a footnote1 . You should take a look—it’s fascinating to read through its reflections.
DeepSeek will hurt Nuclear Power
By now, you’ve probably heard how DeepSeek R1 has disrupted the U.S. AI landscape, giving companies like OpenAI and Anthropic a serious challenge. The biggest surprise? Breaking into the AI game wasn’t as difficult as many assumed. It turns out that newcomers can emerge seemingly out of nowhere and match industry heavyweights like OpenAI and Anthropic.
Now, let’s talk about the electricity demands of these models. Like many others, I used to believe that AI servers would require dedicated nuclear plants just to stay operational. But DeepSeek is doing things differently. Although they’re using Nvidia’s H800 chips, which are inferior to the H100s used by OpenAI and other U.S. firms, DeepSeek claims their model uses 10 to 40 times less electricity than its U.S. counterparts.
This suggests their software is far more efficient. One possible reason? Despite using Nvidia chips, they don’t rely on CUDA, Nvidia’s proprietary software. Instead, they’ve developed their own low-level platform, reportedly called GTX, which communicates with the hardware at the assembly-language level—a much more direct and optimized approach.
If DeepSeek’s claims hold up, and U.S. AI companies adopt similar energy-saving techniques (or if Nvidia integrates them into CUDA), future AI servers might not need dedicated power plants after all. That’s bad news for nuclear power companies, many of which were banking on AI-driven demand to justify new reactor projects.
-+-+-+-+
YouTube Video
Presidential Appointments and RFK Jr.’s Nomination
In the U.S. system, a newly elected President cannot simply appoint Cabinet members and key executive officers. Positions such as the Secretaries of Defense and Treasury, as well as the Directors of the FBI and CIA, require Senate confirmation—a process that demands at least 51 votes.
Recently, Donald Trump nominated Robert F. Kennedy Jr. to lead the Department of Health. Many who rely on mainstream media headlines assume he is an anti-vaccine fanatic. However, having listened to two of his interviews—one on the All-In Podcast and another with Joe Rogan—I find his stance on vaccines to be far more nuanced than what outlets like The New York Times or The Atlantic suggest.
I agree with many of RFK Jr.’s other views on health policy. I was also pleased to see Dr. John Campbell express a similar perspective in support of his nomination.
-+-+-+-+
Diary
Chinese New Year
Both Japanese and Koreans, like the Chinese, traditionally mark the New Year according to the lunar calendar, though their dates vary.
For the Japanese, the Year of the Snake began last Sunday, January 26 (as my Japanese baker informed me). Meanwhile, the Chinese New Year followed three days later, on January 29.
Here is a scene from our local shopping centre:
and starting the Year of the Snake:
In Western religions (Judaism, Christianity, and Islam), the snake is cast as the villain. In contrast, Asian traditions portray it as a symbol of wisdom and thoughtfulness.
We attended New Year dinners—again. Here’s a glimpse of the beautifully set table at the home of a friend we’ve known for over thirty years. The food was delicious, and the evening was wonderful.
We also were invited by Yi’s parents and this was the second feast in one weekend:
As in the Turkish kitchen, the food you cook at home is different from the restaurant feed and I think home cooking is much more interesting and tastier.
Pascal Hagi
We brought the birds inside early today to have the outdoor floor pressure-cleaned. Meliz prepared some food for them, as otherwise, they would have had nothing to eat until morning—apart from the lettuce leaves I clamp to their cage door every afternoon. They were clearly hungry.
Pascal, ever the character, seemed momentarily inclined to acknowledge me with a half-hearted display of dominance. But hunger won out; he abandoned the effort and returned to his meal, murmuring all the while in a language I couldn’t quite decipher..
What I Read
Ursula K Le Guin: Hainish Universe Novels
Rocannon’s World, Planet of Exile, City of Illusions
Ursula K. Le Guin is one of my favorite authors. I remember reading The Left Hand of Darkness, The Dispossessed, and The Beginning Place long ago. More recently, I revisited The Earthsea sequence. Given how much I’ve enjoyed her work, I decided to explore more of her books.
Rocannon’s World was her first novel, set in a future where interstellar travel is limited by the speed of light. Humans discover numerous Earth-like planets with indigenous populations, many of whom resemble humans. The premise is that all these planets were seeded long ago by the planet Hain, forming what Le Guin calls the Hainish Universe.
In this universe, instantaneous communication is possible via a device called the ansible, and inanimate objects can be sent at light speed—making remote bombardments effortless. The protagonist, Rocannon, is a scientist stranded on a planet who must seek local help to escape his predicament.
The Planet of Exile follows a group of Earthmen stranded on a world with an extreme orbit. It takes over 60 Earth years to complete one revolution, leaving the planet in perpetual winter for most of that time. The settlers must navigate complex interactions with a local race while facing a more feral species that threatens both groups’ survival.
City of Illusions is a classic Stranger-in-a-Strange-Land story. A man with no memory is thrust into a future world, searching for his identity and purpose. Most people he encounters deceive him for their own reasons, raising questions about truth and perception. In this book, his convictions, guided by instinct rather than reason, shape his journey. It presents an intriguing philosophical dilemma.
All three books are accessible reads. If you’re short on time, you can safely skip Rocannon’s World and still enjoy the other two.
Stephen Baxter, Galaxias
Stephen Baxter is another favorite of mine, but Galaxias was a disappointment. The premise is intriguing: an advanced alien species monitors emerging civilizations and suppresses interstellar travel. When Pioneer 10 became the first human-made object to leave the solar system in 1973, it went unnoticed—until 2057, when humanity receives an unmistakable warning: the Sun vanishes.
The idea of a controller species enforcing isolation is reminiscent of Baxter’s Creation Node, but I found the execution in that book more compelling. Galaxias spends most of its pages on governmental and international deliberations over how to respond to an entity capable of moving the Sun. While political narratives can sometimes be engaging, the treatment here is perfunctory and uninspired. The result is a dull, frustrating read.
Hōsuke Nojiri, Usurper of the Sun
Hōsuke Nojiri, a Japanese game designer and science fiction writer, presents a more engaging take on an alien intervention. In Usurper of the Sun, a super-advanced race begins constructing a massive ring around the Sun, oblivious to humanity’s existence. The resulting shadow wreaks havoc on Earth’s ecology, forcing humanity into a desperate, stumbling response.
Unlike Galaxias, this book keeps the reader engaged with its likable characters and well-paced narrative twists. I thoroughly enjoyed it.
Fredrik Bakman, The Answer is No
I read The Answer is No on Yi’s recommendation, and I’m glad I did. Backman wasn’t on my radar, but he’s apparently a rising star. The Sydney Morning Herald even calls him Sweden’s most popular literary export since Stieg Larsson (The Girl with the Dragon Tattoo).
More a story than a novel—what once might have been called a novella—it’s available on Kindle for A$3.18.
The protagonist, Lucas, is a young software professional who works from home, which suits him well since he dislikes social interaction. But living in an apartment comes with the unavoidable risk of encountering neighbors. The book’s observations on human relationships aren’t necessarily profound, but they’re insightful, amusing, and relatable. I enjoyed it and might pick up Backman’s breakthrough novel, A Man Called Ove, next..
-+-+-+-+
Comparing Istanbul and Brisbane prices - AT index
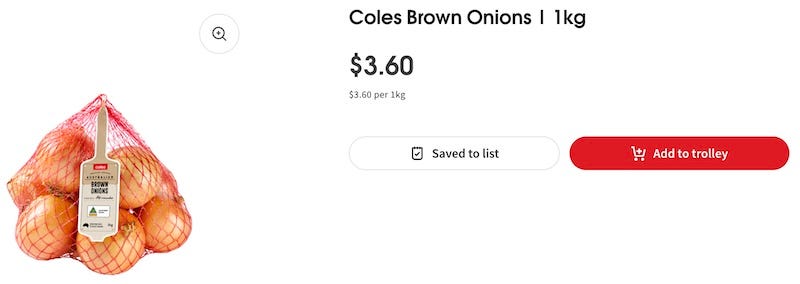
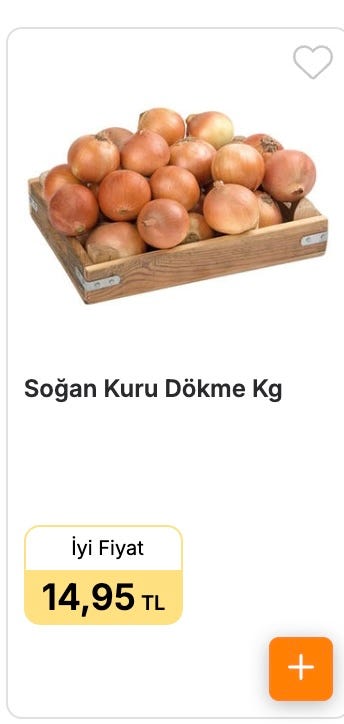
Based on my basket of goods, Australia is 45% more expensive this week compared to Istanbul. Both Coles (AU) and Migros (TR) prices are expressed in Turkish liras for the items in the basket on 3 February 2025. I converted Coles prices to Turkish liras at the exchange rate of 1AUD=22.09 TRY.
The y-axis in the following chart is
The trend (the red dotted line) is rising, which means that, since 5 July 2024, the Turkish prices are slowly approaching the Australian prices. Some items, e.g. beef mince, is more expensive than in Brisbane and has been consistently so since I started this chart.
The index is not very smart and a large change in one item may dominate the final result. This week, there was a big difference in the price of the onions.
The code to create the above tables and the plot is in my github repository and can be downloaded if you are interested.
Question:
DeepSeek Thinking :
Okay, so I need to find the cross-sectional area of a cantilever beam that has a circular cross-section with a diameter of 10 mm. Hmm, cross-sectional area for a circle... I remember it's something with pi and radius squared. Let me think. The formula for the area of a circle is A = πr², right? Yeah, that sounds familiar from geometry.
But wait, the problem gives me the diameter, not the radius. So I should remember that the radius is half of the diameter. The diameter is 10 mm, so the radius would be 10 divided by 2, which is 5 mm. Got that. So radius r = 5 mm.
Now plug that into the area formula. A = π*(5 mm)². Let me calculate that. 5 squared is 25, so it becomes π*25 mm². So the area is 25π square millimeters. Is that all? Seems straightforward.
Wait, but maybe I need to convert the units? The question doesn't specify, but since the diameter is given in millimeters, the area should be in square millimeters. Unless they want it in another unit like meters or centimeters, but the problem doesn't say. Probably safe to leave it in mm².
Let me double-check the formula. Area of a circle is πr². Yes, radius is half of diameter. So diameter 10 mm, radius 5 mm. Squared is 25. Multiply by pi. 25π mm². That should be the answer.
Alternatively, if they want a numerical value instead of leaving it in terms of pi, I can compute that. Pi is approximately 3.1416. So 25*3.1416 = 78.54 mm². But the question doesn't specify whether to use π or a numerical approximation. Since it's an engineering question, maybe they want the exact value in terms of pi. Hmm.
Looking back at the problem statement: "What is its cross-sectional area?" It doesn't specify, but in engineering contexts, sometimes they prefer exact terms with pi for precision, especially if it's for further calculations. But sometimes they want a decimal number. Since the diameter is given as a whole number, 10 mm, maybe 25π mm² is acceptable. But just to be thorough, maybe present both? Wait, but the problem might expect just the exact value.
Alternatively, maybe they want the answer in standard units like meters. But 10 mm is 0.01 meters, so radius would be 0.005 meters. Then area would be π*(0.005)^2 = π*0.000025 m² = 25π x 10^-6 m². But that seems unnecessarily complicated. The question is in millimeters, so unless specified, stay in millimeters.
I think 25π mm² is the correct answer here. Let me check with an example. If diameter is 2 mm, radius 1 mm, area is π*1²=π mm². So yeah, same logic. So 10 mm diameter, 5 mm radius, area 25π mm². That seems right.
Alternatively, maybe the question is a trick question? Like, is the cross-sectional area different because it's a cantilever beam? Wait, no. Cross-sectional area is just the area of the shape, regardless of the beam type. Cantilever just refers to how it's supported, fixed at one end. Doesn't affect the cross-sectional area. So the answer is purely based on the geometry.
Therefore, I think confidently the cross-sectional area is π multiplied by radius squared, which is 25π mm². If I have to give a numerical value, approximately 78.54 mm², but since the problem didn't specify, probably the exact form is better.
**Final Answer**
The cross-sectional area of the cantilever beam is \boxed{25\pi} square millimeters.
Answer:
Second question:
DeepSeek Thinking :
Okay, so the user asked about the maximum stress in a cantilever beam. Let me start by recalling what I know about cantilever beams. A cantilever is a beam that's fixed at one end and free at the other, right? When a load is applied at the free end, it causes bending. The maximum stress in such a case is called the bending stress, which I think is calculated using the formula σ = (M * y) / I, where M is the bending moment, y is the distance from the neutral axis to the outermost fiber, and I is the moment of inertia of the cross-section.
Wait, but the user mentioned the beam has a circular cross-section with a diameter of 10 mm. So, I need to make sure I use the correct moment of inertia for a circle. The moment of inertia for a circular section is I = (π * d^4)/64, where d is the diameter. Alternatively, since the radius is 5 mm, maybe it's also expressed in terms of radius: I = (π * r^4)/4. Let me check that. Hmm, no, actually, the formula using diameter is I = π * d^4 / 64, and using radius is I = π * r^4 / 4. So if the diameter is 10 mm, then radius is 5 mm. So maybe I should use the radius version here.
But let's confirm. The moment of inertia for a circular section about the neutral axis is indeed I = (π * d^4)/64 when using diameter. So that's probably safer here since the diameter is given. So substituting d = 10 mm, I = π * (10)^4 / 64. Let's compute that.
But first, the bending moment M. Since it's a cantilever beam with a point load at the end, the bending moment at the fixed end (which is where the maximum moment occurs) is M = F * L, where F is the force and L is the length. The user said the length is 1 m, which is 1000 mm, and the force is 100 N. So M = 100 N * 1000 mm. Wait, but units here need to be consistent. The length in meters is 1 m, so perhaps better to convert length to meters. But the diameter is in mm. Hmm, maybe convert all units to meters to keep consistent. Alternatively, since stress is in Pascals (N/m²), we need to make sure all units are in meters and Newtons.
Wait, let's outline the steps clearly:
1. Calculate the bending moment M = F * L. F is 100 N, L is 1 m. So M = 100 N * 1 m = 100 N·m.
2. Calculate the section modulus Z, which is I / y. For a circular cross-section, the section modulus Z is given by Z = (π * d³) / 32. Alternatively, since y is the distance from the neutral axis to the outer fiber, which is half the diameter, so y = d/2 = 5 mm = 0.005 m. Then Z = I / y. Let me verify.
Wait, the section modulus Z is indeed equal to I / y. For a circular cross-section, I = (π * d^4)/64, and y = d/2. So Z = (π * d^4 / 64) / (d/2) ) = (π * d^3) / 32. So Z = π * d³ / 32. That's correct.
So maybe using Z is easier here. Then the maximum bending stress σ = M / Z.
So let's compute Z first. The diameter d is 10 mm, which is 0.01 meters. So Z = π * (0.01 m)^3 / 32.
Calculating that: (0.01)^3 = 1e-6 m³, so Z = π * 1e-6 / 32 ≈ 9.817e-8 m³.
Then, M is 100 N·m. So σ = 100 N·m / 9.817e-8 m³ ≈ 1.0186e9 Pa, which is approximately 1.019 GPa. That seems really high. Wait, but steel's yield strength is around 250 MPa, so this stress would be way beyond that. Maybe I made a mistake in units.
Wait a second, perhaps I messed up the unit conversions. Let's check again.
The diameter is 10 mm, which is 0.01 meters. So in meters, that's correct. But when calculating Z = π * d³ / 32, with d in meters, the unit for Z would be m³. Then M is in N·m. So σ = M / Z would be (N·m) / (m³) = N/m², which is Pa. That's correct.
But 100 N·m divided by ~9.8e-8 m³ gives around 1.02e9 Pa, which is 1.02 GPa. That does seem extremely high. Maybe I made an error in calculation steps.
Alternatively, perhaps the user is expecting the answer in MPa, but regardless, the calculation seems correct. Let me cross-verify using another approach.
Alternatively, compute the moment of inertia I first. I = π * d^4 / 64. So d = 10 mm = 0.01 m. So I = π * (0.01)^4 / 64. (0.01)^4 = 1e-8 m^4. So I = π * 1e-8 / 64 ≈ 4.9087e-10 m^4.
Then, y = d/2 = 0.005 m.
So σ = (M * y) / I = (100 N·m * 0.005 m) / 4.9087e-10 m^4 = (0.5 N·m²) / 4.9087e-10 m^4 ≈ 1.0186e9 Pa, same as before. So same result.
But wait, maybe the user intended the diameter to be in mm, but the formula requires meters. Alternatively, maybe the user expects the answer in N/mm², which would be MPa. Let me try calculating in mm.
Let's redo the calculation using mm throughout.
M = F * L = 100 N * 1000 mm = 100,000 N·mm.
I = π * d^4 / 64 = π * (10 mm)^4 / 64 = π * 10000 / 64 mm^4 ≈ π * 156.25 mm^4 ≈ 490.87 mm^4.
y = 5 mm.
σ = (M * y) / I = (100,000 N·mm * 5 mm) / 490.87 mm^4 = (500,000 N·mm²) / 490.87 mm^4 ≈ 1018.6 N/mm².
Since 1 N/mm² = 1 MPa, this is 1018.6 MPa, which is the same as 1.0186 GPa. Same result. So yes, the calculation is correct. But this stress is indeed very high, which would likely exceed the yield strength of common materials. However, the question is purely theoretical, so the answer is just based on the given values.
Therefore, the maximum stress caused in the beam is approximately 1.019 GPa, which can be written as 1018.6 MPa or rounded to 1020 MPa. However, the exact value using exact computation would be (100 * 1000 * 5) / (π * 10^4 / 64) = (5,000,000) / (π * 10,000 / 64) ) = (5,000,000 * 64) / (π * 10,000) ) = (320,000,000) / (10,000 π) ) = 32,000 / π ≈ 10,186.1 N/mm² ≈ 101.86 MPa? Wait, wait, hold on. Did I mess up the calculation here?
Wait, let's recalculate using mm units:
M = 100 N * 1000 mm = 100,000 N·mm.
I = π * (10 mm)^4 / 64 = π * 10,000 mm^4 / 64 = (10,000 / 64) * π ≈ 156.25 * π ≈ 490.8737 mm^4.
y = 5 mm.
σ = (M * y) / I = (100,000 * 5) / 490.8737 ≈ 500,000 / 490.8737 ≈ 1018.59 N/mm².
Which is 1018.59 MPa, as before. So why did I get confused earlier when I thought 1018 MPa is 1.018 GPa? Yes, that's correct.
But maybe the user made a mistake in the numbers? If the diameter was 10 cm (100 mm), the stress would be much lower. But given the problem states 10 mm diameter, the calculation is correct.
Alternatively, maybe the user intended to ask for the cross-sectional area, which was the previous question, but now moving on to stress. But given the problem as stated, the answer is correct.
Therefore, the maximum stress is approximately 1018.6 MPa, which can be boxed as 1020 MPa or expressed in terms of π. Wait, let's see:
Wait, let's express the answer symbolically first. The formula is σ = (32 * F * L) / (π * d³). Because:
σ = M / Z, and M = F * L, Z = π d³ / 32.
Therefore, σ = (F * L) / (π d³ / 32) ) = 32 F L / (π d³).
Plugging in F = 100 N, L = 1 m = 1000 mm, but wait, need to keep units consistent. If L is in meters and d is in meters:
L = 1 m, d = 0.01 m.
σ = 32 * 100 N * 1 m / (π * (0.01 m)^3 ) = 3200 / (π * 1e-6) ≈ 3200 / 3.1416e-6 ≈ 1.0186e9 Pa.
Same as before. So the exact expression is σ = (32 * F * L) / (π d³). If we want to present it in terms of π, it's 3200 / π MPa, but usually, we'd compute the numerical value.
Thus, the final answer is approximately 1020 MPa. However, if we want to keep it exact, we can write 32000/(π) MPa since:
Wait, 32 * 100 N * 1 m = 3200 N·m.
But d is 0.01 m, so d³ = 1e-6 m³.
Thus, 3200 / (π * 1e-6) = 3200 / 1e-6 / π = 3.2e9 / π Pa. So 3.2e9 / π Pa ≈ 1.0186e9 Pa ≈ 1.019 GPa. Alternatively, 3.2e9 / π Pa is equivalent to 3.2e3 / π MPa ≈ 1018.59 MPa.
But in the box, probably better to write the numerical value as approximately 1020 MPa or 1.02 GPa. However, to be precise, it's exactly (32 * 100 * 1) / (π * 0.01³) Pa. Let me compute that:
32 * 100 = 3200.
0.01³ = 0.000001.
So denominator is π * 0.000001 ≈ 3.1415926536e-6.
3200 / 3.1415926536e-6 ≈ 3200 / 0.0000031415926536 ≈ 1,018,591,635.8 Pa ≈ 1.0186e9 Pa ≈ 1018.6 MPa.
So, the precise answer is approximately 1018.6 MPa, which can be rounded to 1019 MPa or 1.02 GPa. Depending on the desired precision, but in engineering contexts, three significant figures might be appropriate. So 1.02 × 10³ MPa, which is 1.02 GPa.
But the problem didn't specify material or anything else, so just the calculation based on given numbers. Therefore, the maximum stress is 32 * F * L / (π * d³). Substituting F=100N, L=1m, d=0.01m, gives 1018.59 MPa. So boxed as \boxed{1019 \text{ MPa}} or \boxed{1.02 \times 10^3 \text{ MPa}}.
Alternatively, maybe the problem expects an exact expression in terms of π. Let's see:
σ = 32 * F * L / (π * d³) = 32 * 100 N * 1 m / (π * (0.01 m)^3) = 3200 / (π * 1e-6) Pa = 3.2e9 / π Pa. So if expressed as a multiple of 1/π, it's (3.2e9)/π Pa, but that's not commonly done. Typically, you compute the numerical value.
Therefore, the answer is approximately 1019 MPa. So box that.
This is a fascinating soliloquy. At the end, it gets the correct answer and “boxes” it:
Answer: