Claude and ChatGPT

I asked them to calculate the bending stress for a cantilever beam

Today, I tried a simple engineering problem with ChatGPT and Claude. It is not a fair comparison because I have a paid ChatGPT subscription but am using free Claude. I post this comparison because I thought the way Claude errs in the response is illustrative. I use a Chain-Of-Thoughts prompting strategy, which is a technique used in large language models (LLMs) to break down complex reasoning tasks into a series of intermediate steps, making the reasoning process more transparent and easier to follow. From its explanation of intermediate calculations, one can see that Claude was able to dig up the correct equations but uses them incorrectly.

Problem

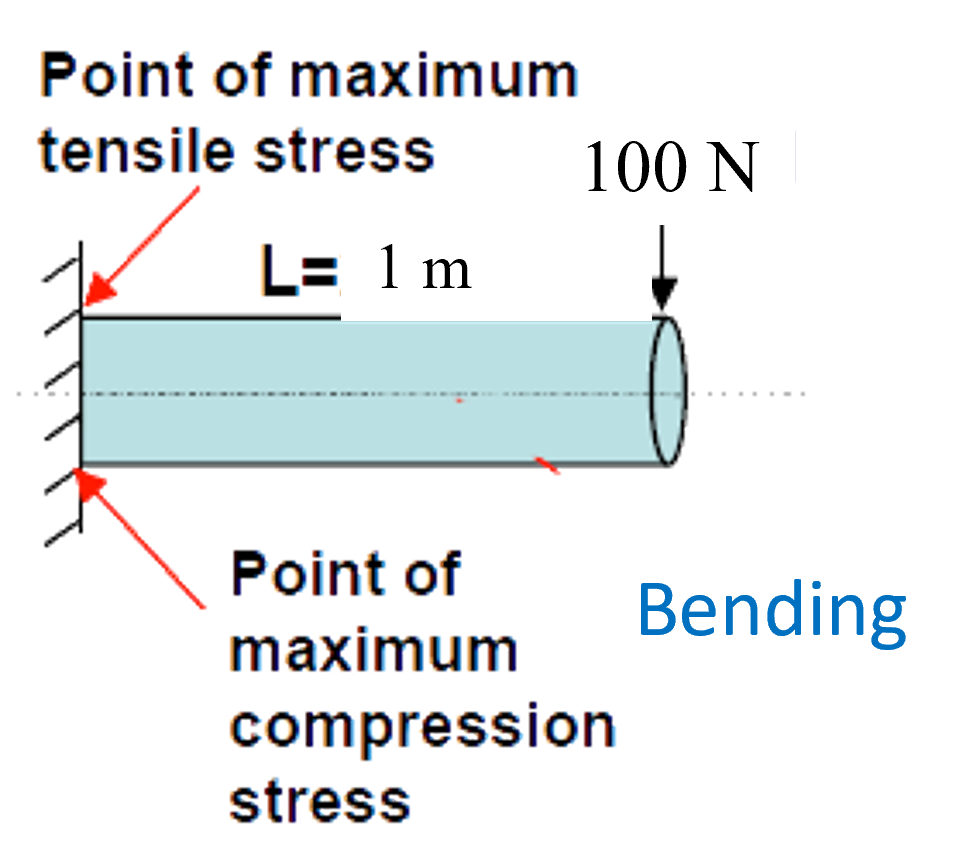
I asked both models to calculate the maximum stress for a cantilever beam subject to a load applied at its free end. The following image is for your convenience. To Claude and ChatGPT, I described the problem in text only.

I asked the problem in two stages:

• First, I only supplied the beam diameter and asked them to compute the cross-sectional area

• Then, I supplied the length of the beam and the magnitude of the applied load and asked them to calculate the bending stress.

I copy my prompts and the model responses below:

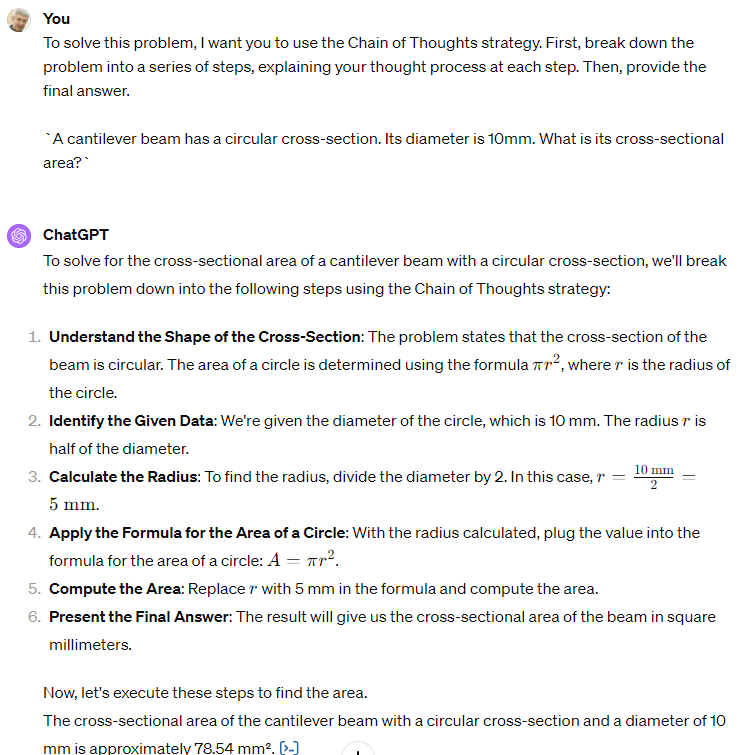
ChatGPT answer

First the cross-sectional area:

The answer is correct.

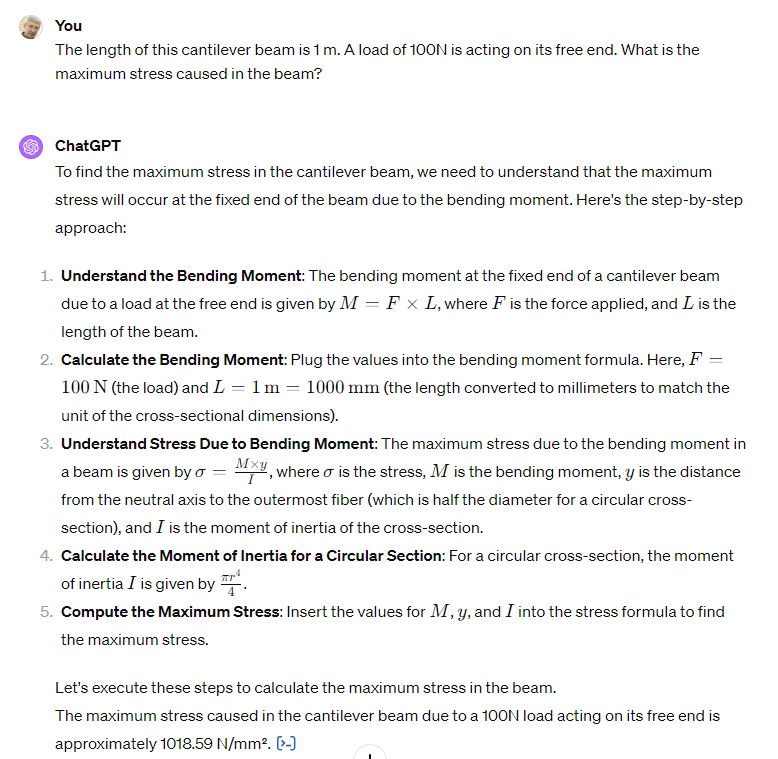
Then I asked ChatGPT to compute bending stress:

The answer is correct.

---

Let us now try the same problem with Claude. As I said above, it is not a fair comparison because I am comparing a free version (Claude) against a paid subscription (ChatGPT). Nevertheless, here is what Claude says.

Claude answer

I gave exactly the same prompts. First, the area:

This is the correct answer. Now the bending stress:

Conclusion

Both ChatGPT and Claude explained their intermediate steps and arrived the same answer of 78.54 mm^2, which is the correct answer.

I then asked "The length of this cantilever beam is 1 m. A load of 100N is acting on its free end. What is the maximum stress caused in the beam?"

Both Claude and ChatGPT went through the correct reasoning. But Claude made a mistake in calculating the moment of inertia I (it used the correct formula as I= (π × r^4) / 4) but computed the result as 1963.5 mm^4.

What I found most interesting in the above was Claude picking the correct equation but making an error in its application.

My Python script

Here is my python script that I used to check the LLM results:

PI=3.14159 # Value of pi
d=0.01 # Diameter of a circular rod, m
A=PI*(d/2)**2 # Cross-sectional area of the rod, m^2
I=PI*d**4/64 # Moment of inertia of the rod, m^4
I2=(PI*(d/2)**4)/4 # Moment of inertia of the rod, m^4
F=100 # Force applied at the free end of the cantilever, N
L=1 # Length of the rod, m
M=F*L # Moment applied at the fixed end of the cantilever, Nm
sigma=M*(d/2)/I # Bending stress at the fixed end of the cantilever, Pa
print(A*1e6, I, I2, sigma/1.e6)